In this example we demonstrate the dispersion characteristic obtained for a plane electromagnetic wave propagating in unbound magnetic dielectric medium. The numerical solution is produced by MaxLLG and compared with the analytical formulation derived for a linearised solution of LLG equation [1]. The wave is linearly polarised and propagates in the direction parallel to the magnetic field ![]() and Magnetisation
and Magnetisation ![]() (aligned with axis y). The electric conductivity of the medium
(aligned with axis y). The electric conductivity of the medium ![]() is zero and the relative permittivity
is zero and the relative permittivity ![]() is constant. The analytical dispersion relation is
is constant. The analytical dispersion relation is
(1) ![]()
where ![]() is the propagation constant for the light and
is the propagation constant for the light and ![]() are the effective permeabilities of tangentially magnetized ferrite for right hand circular mode
are the effective permeabilities of tangentially magnetized ferrite for right hand circular mode
(2) ![]()
and for left hand circular mode
(3) ![]()
[1] where ![]() and
and ![]() are diagonal and off-diagonal (gyrotropic) components of the permeability tenzor,
are diagonal and off-diagonal (gyrotropic) components of the permeability tenzor, ![]() is the resonance frequency, H is the applied magnetic field,
is the resonance frequency, H is the applied magnetic field, ![]() ,
, ![]() is the saturation magnetization,
is the saturation magnetization, ![]() – gyromagnetic ratio. Thus, the dispersion relation can be rewritten as:
– gyromagnetic ratio. Thus, the dispersion relation can be rewritten as:
(4) ![]()
The equation (4) is based on the linearised solution of Landau-Lifshits-Gilbert equation [1] with the dispersion curve shown on figure 1(d). Note, this equation does not allow for an explicit functional relation but a numerical formulation (to any degree of precision) can be easily done (figure 1(d) red line).
As in other case studies, the first step in simulating the dispersion of the waves propagating in the unbounded ferrite is to create an input file of the media. In case of long structures having the same cross-sections it is easier to use 2D formulation. For this purpose one can upload a png image of the model cross-section to the 2D Image Files section (make sure to avoid anti-aliasing effects normally present in all modern graphic editors. Each colour should represent only one particular material). The picture made for the given example is shown in figure 1(a). All sizes are set in pixels (px) and the picture shows two regions corresponding to different materials: ferrite (green square) and air (blue area). The latter is necessary to include the periodic boundary condition (PBC) or Perfectly Matched Layer (PML) which are needed to either replicate the given geometry to an infinite extent or use absorbing layers accordingly. In this particular example we use the following dimensions and parameters given in figures 1(a) and 1(b) accordingly. Once the matrix file is created, the next step is to set parameters in the metascript file. In this case the medium was excited with the magnetic field pulse located in y = 500, all cell sizes were 0.2 mm, and the applied field was aligned with axis y. To have ferrite unbounded the PBC were set for all orientations.
During simulation MaxLLG takes field intensity maps in the medium planes every Nth frame, where N is set at the Parameters step figure 1(c). When the simulation is complete, an array of field profiles along y axis at fixed point x0 for each frame is taken and combined chronologically in a new space-time map (only for one particular orientation where profiles are collected – this is the orientation of the sought dispersion). So a time map is made where the field evolution in the structure is seen (inclusion in figure 1(c)). The figure 1(d) demonstrates the results of the two-dimensional Fourier transform of the space-time map compared with the analytical ones obtained using (1-3). One can see that dispersion curves of two right hand circular modes (red lines) and the left hand circular mode (blue line) very well correlate with the numerical solution (yellow points).
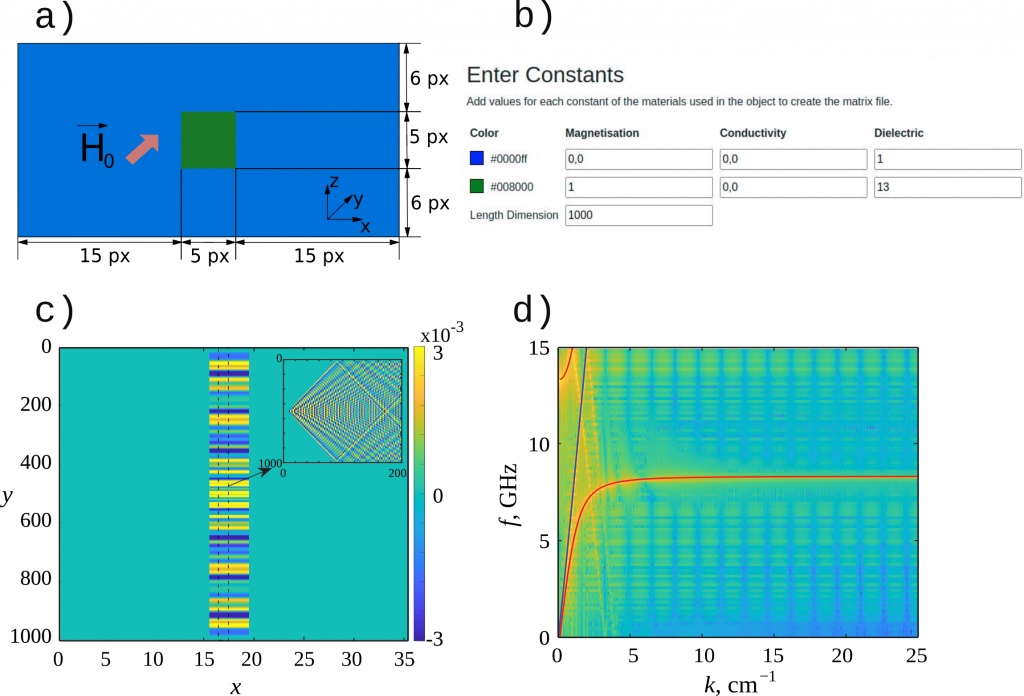
Fig. 1. a) Image of the model cross-section showing two regions corresponding to different materials: ferrite (green square) and air (blue area). b) Medium parameters used in the simulation. c) A field intensity map taken in x-y plane, and a space-time map collected of field profiles at point ![]() 17 px (inclusion). d) The dispersion characteristic obtained for a plane electromagnetic wave propagating in unbound magnetic dielectric medium by means of MaxLLG (yellow points) and the analytical formulation (red lines and blue line correspond to right and left hand circular modes accordingly) with parameters:
17 px (inclusion). d) The dispersion characteristic obtained for a plane electromagnetic wave propagating in unbound magnetic dielectric medium by means of MaxLLG (yellow points) and the analytical formulation (red lines and blue line correspond to right and left hand circular modes accordingly) with parameters: ![]() kOe,
kOe, ![]() kOe,
kOe, ![]() ,
, ![]() .
.
[1] Gurevich A.G., Melkov G.A. Magnetization Oscillations and Waves. CRC Press, Inc; 1996. 445 p.